単振動とは、ある位置を中心に振動をする運動のことである。
よって、単振動は三角関数で表す事ができる。
単振動の特徴は、単振動の運動を大きく決める振動数と周期が物体の質量や振幅に依らないことである。
振動数と周期は運動方程式を立てることで求めることができる。
本記事では単振動について説明する。
単振動と円運動
単振動は物体がある位置を中心にして振動をする運動である。
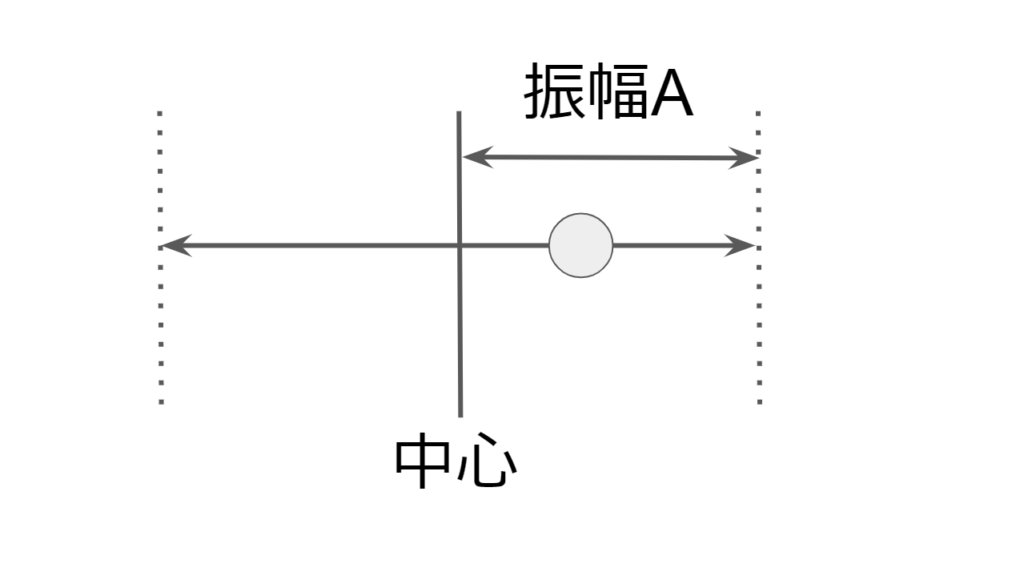
この時、中心から最大の位置との距離を振幅と呼ぶ。
単振動は以下の様に円運動の縦方向の運動と考える事ができる。
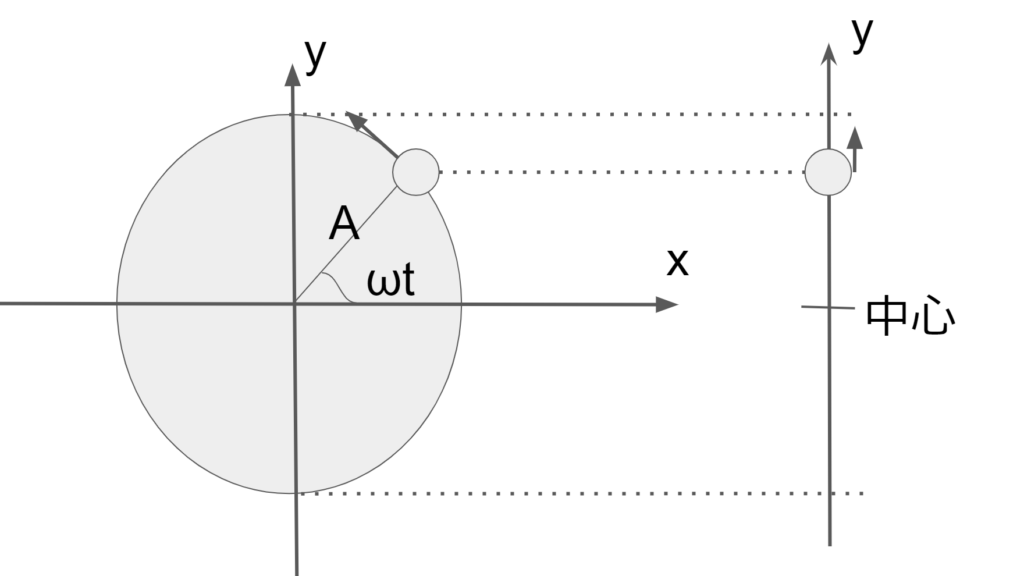
この時、単振動は円運動の\(y\)方向のみを考えるので位置座標は以下になる。
\begin{eqnarray}
&&y=A\sin\left(\omega t+\theta_0\right)\\
\\
\omega&:&振動数(次章で説明)\\
A&:&円運動の半径であり、単振動の振幅\\
\theta_0&:&t=0でのx軸とOPなす角度
\end{eqnarray}
また、円運動では常に円の中心に向かって力が働いていた。
よって、単振動でも常に振動の中心に向かって円運動の力の\(y\)方向の力\(F_y\)が働く。
\begin{eqnarray}
F_y&=&-mA\omega^2\sin\left(\omega t+\theta_0\right)\\
\\
&=&-m\omega^2y\\
\\
m&:&質量
\end{eqnarray}
【円運動とは】
単振動の例)
単振り子、バネの振動
単振動の運動方程式
単振動の運動方程式を考える。
前章で求めた\(y,F_y\)を用いて、運動方程式は以下になる。
\begin{eqnarray}
m\frac{d^2y}{dt^2}=-m\omega^2y\\
\end{eqnarray}
ここで、振動数\(\omega\)の意味について考える。
位置座標\(y=A\sin\left(\omega t+\theta_0\right)\)より、円運動では単位時間当たりに回転する角度(時間\(t\)の間に\(\omega t\)だけ回転)を表す。
よって、単振動では単位時間あたりに振動する回数を表す。
つまり、\(\omega\)が大きいほど高速で振動をする。
ここで、運動方程式から\(m\)を消去した以下の等式を考える。
\begin{eqnarray}
\frac{dy}{dt^2}=-\omega^2y
\end{eqnarray}
この\(\omega\)は加速度(位置座標の二階微分)の係数が\(1\)、右辺の位置座標の係数に\(-\)がついている時、位置座標の\(-\)を除いた係数が\(\omega^2\)になる。
言い換えれば、物体にかかる力が\(-ky\)(\(k\)は定数)の時、物体は単振動をして、振動数の2乗は\(\frac{k}{m}\)となる。
力が\(-ky\)の時の運動方程式は以下になる。
\begin{eqnarray}
m\frac{dy}{dt^2}=-ky
\end{eqnarray}
この時の\(-ky\)を復元力と呼ぶ。
【微分とは】
【復元力の例であるバネの弾性力】
また、単振動の周期を考える。
周期を\(T\)とすると、振動数との関係から以下を満たす。
\begin{eqnarray}
\omega T=2\pi
\end{eqnarray}
この\(\omega,T\)は物体の質量\(m\)と復元力の定数\(k\)だけに依存して、振幅や位置座標には依存しない。
また、単振動はバネを物体に取り付けた時の運動と同じなので、以下の様にバネの弾性エネルギーと同じである。
\begin{eqnarray}
U=\frac{1}{2}ky^2
\end{eqnarray}

