円運動とは物体が円を描きながら運動をすることである。
円運動の特徴は、物体にかかる力は常に円の中心を向いていることである。
これらの円運動の例として天体の運動がある。
天体間には万有引力が働いており、この万有引力によって天体は円を描きながら運動をする。
本記事では円運動と万有引力について説明する。
円運動
円運動は円の中心からの距離が一定であり、円の中心を回る運動である。
位置、速度、加速度
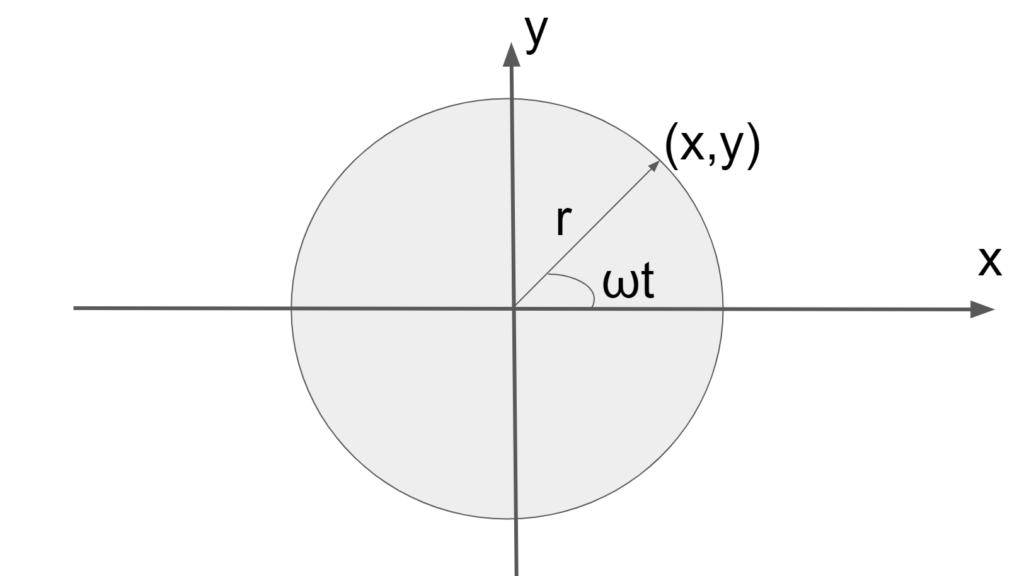
円運動の位置座標の時間変化を考える。
円軌道の中心を\(xy\)平面の原点とすると円運動の位置座標の時間変化はそれぞれ以下になる。
\begin{eqnarray}
\overrightarrow{X}&=&\left(r\cos\omega t,r\sin\omega t\right)\\
\\
\overrightarrow{X}&:&位置座標ベクトル\\
r&:&円軌道の半径\\
\omega&:&角速度(単位時間あたりに回転する角度)\\
t&:&時間
\end{eqnarray}
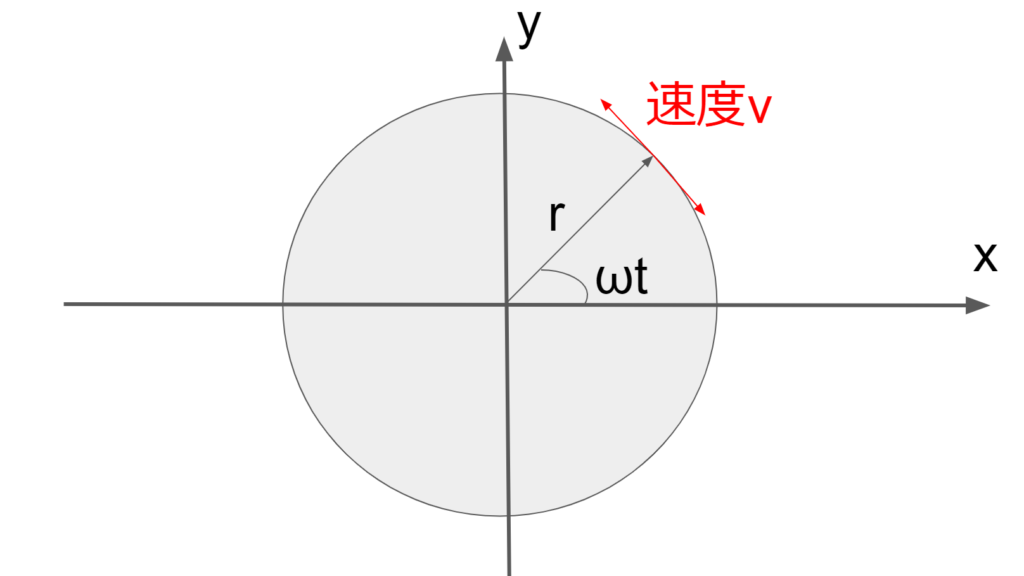
この位置座標から速度\(v\)を考える。
速度\(v\)は位置座標の導関数なので速度\(v\)は以下になる。
\begin{eqnarray}
\overrightarrow{v}=\frac{d\overrightarrow{X}}{dt}=r\omega\left(-\sin\omega t,\cos\omega t\right)
\end{eqnarray}
この速度の大きさ\(|v|\)は\(r\omega\)であり時間に依らず一定である。
また、位置座標ベクトル\(\overrightarrow{X}\)と速度\(\overrightarrow{v}\)の内積は以下になる。
\begin{eqnarray}
\overrightarrow{v}\cdot\overrightarrow{X}=0
\end{eqnarray}
よって、速度の向きは位置座標ベクトルに対して90°の角度をなしている、つまり、円運動の軌道の接線方向であることが分かる。
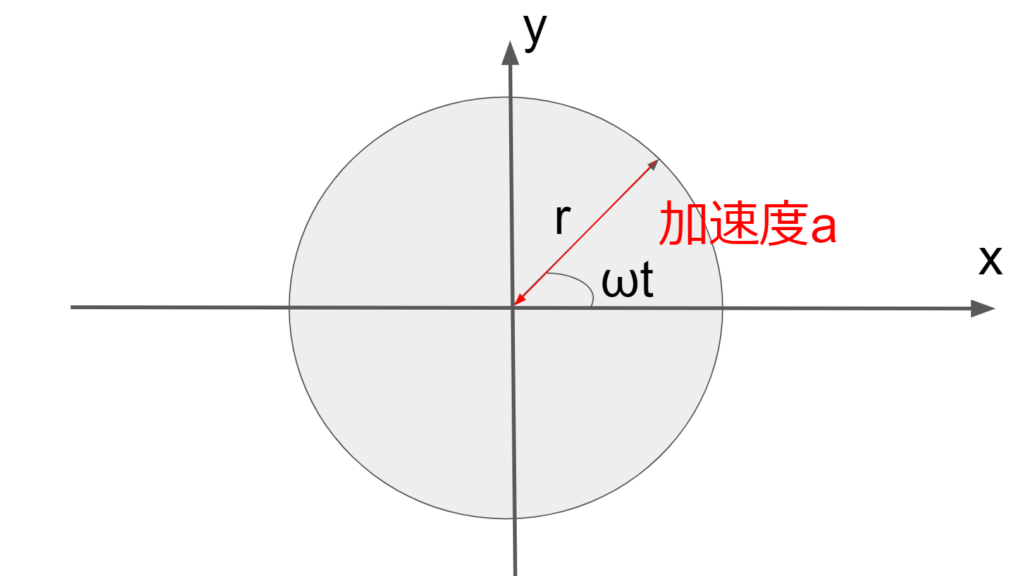
次に円運動の加速度を考える。
加速度\(\overrightarrow{a}\)は速度ベクトル\(\overrightarrow{v}\)の導関数であるので以下になる。
\begin{eqnarray}
\overrightarrow{a}&=&\frac{d\overrightarrow{v}}{dt}=-r\omega^2\left(\cos\omega t,\sin\omega t\right)\\
\\
&=&\omega^2\left(-\overrightarrow{X}\right)
\end{eqnarray}
よって、円運動の時の加速度の大きさは\(r\omega^2\)であり、方向は位置座標ベクトルの向きの逆方向、つまり、円の中心方向であることが分かる。
【円の方程式】
【位置、速度、加速度の関係】
運動方程式
円運動の運動方程式を考える。
円運動では、極座標で考えたほうがわかりやすいので極座標で運動方程式を考える。
更に、物体に力が働く方向は\(r\)方向のみなので、\(r\)方向のみの運動方程式を立てる。
すると、以下になる。
\begin{eqnarray}
&&-mr\omega^2=F\\
\\
m&:&質量\\
F&:&物体にかかる力(+r方向を正とする)
\end{eqnarray}
以上から物体にかかる力は円の中心を向いていることが分かる。
よって加速度の大きさと力の大きさによる運動方程式は以下である。
\begin{eqnarray}
mr\omega^2=F
\end{eqnarray}
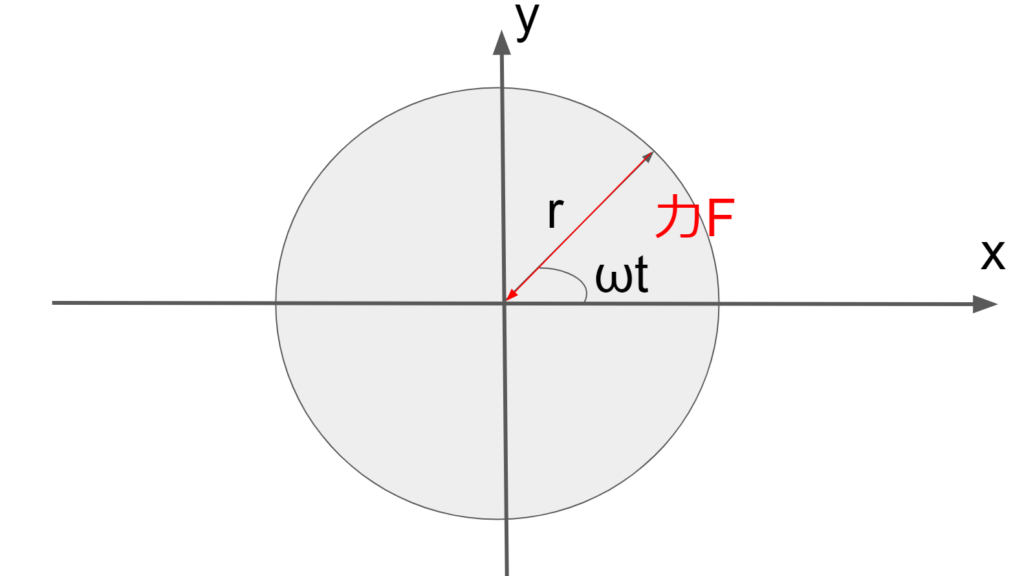
以上のように物体にかかる力が常に円の中心方向を向いている円運動の例として天体の運動がある。
次章では、質量を持つ物体同士に働く万有引力についてい説明する。
万有引力
万有引力の法則
万有引力は2物体間に働く引力である。
この万有引力は2物体の質量の積に比例して、2物体間の距離の2乗に反比例する。
\begin{eqnarray}
F&=&G\frac{m_1m_2}{r^2}\\
\\
F&:&万有引力\\
G&:&万有引力定数\\
r&:&2物体間の距離\\
m_1,m_2&:&物体の質量
\end{eqnarray}
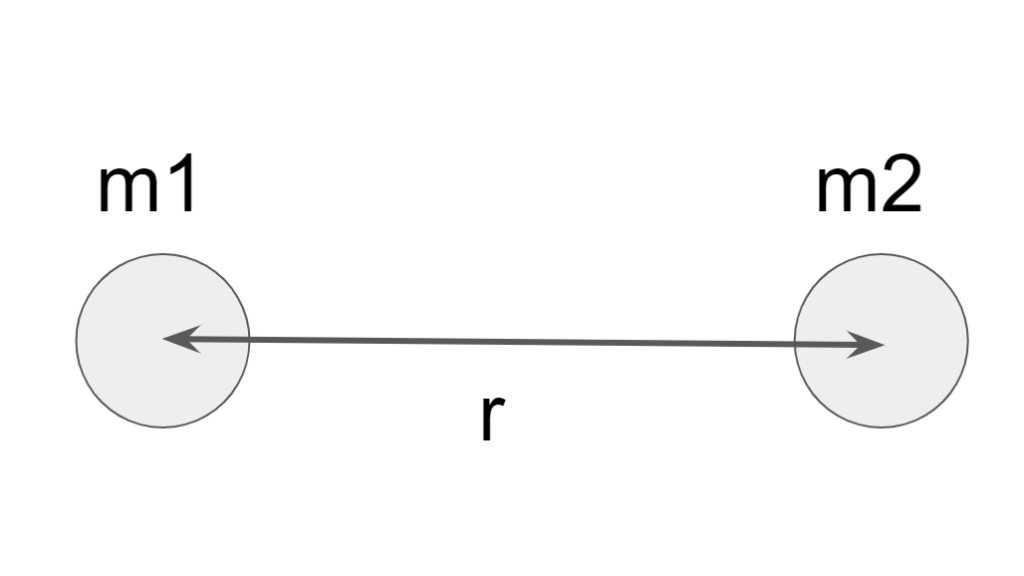
このとき、2物体の内の一つの物体を地球として考える。
地球の質量を\(M\)、地球の半径を\(R\)とすると、地球の表面上にある物体にかかる万有引力は以下になる。
\begin{eqnarray}
F&=&\underbrace{\frac{GM}{R^2}}_{重力加速度g}m_2\\
\\
&=&m_2g
\end{eqnarray}
この時、\(\frac{GM}{R^2}=g\)とすると、万有引力は\(F=m_2g\)となる。
この時の\(g\)を重力加速度と呼び、この時の万有引力を重力と呼ぶ。
また、地球以外の天体の重力を考える時は、それらの天体の質量と半径を考えて万有引力を求めれば良い。
万有引力の位置エネルギー
万有引力による位置エネルギーを考える。
位置エネルギーは万有引力によるポテンシャルなので以下になる。
\begin{eqnarray}
U&=&-\int_{r_0}^{r}G\frac{Mm}{r’^2}dr’\\
\\
&=&-GMm\left(\frac{1}{r}-\frac{1}{r_0}\right)\\
\\
U&:&ポテンシャル(位置エネルギー)\\
M,m&:&物体の質量\\
r_0&:&基準点の位置\\
r&:&物体間の距離
\end{eqnarray}
ここで、基準点を\(r_0=\infty\)の極限を取るとポテンシャル\(U\)は以下になる。
\begin{eqnarray}
U=-G\frac{Mm}{r}
\end{eqnarray}
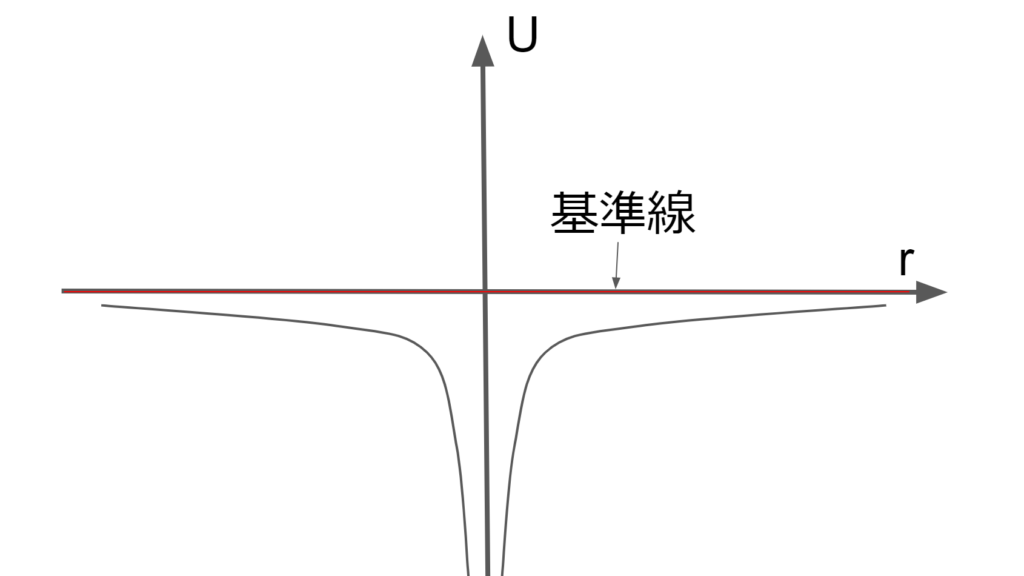
この万有引力の位置エネルギーから分かることは、質量\(M\)の物体によって質量\(m\)の物体が束縛されていることである。(又は、その逆)
ポテンシャル\(U\)のグラフを見ると、物体間の距離が短いほどポテンシャル\(U\)は小さくなる。
ポテンシャル\(U\)が小さくなるほど物体は安定状態になるので、常に物体間の距離は短くあろうとする。(少なくとも、物体にエネルギーを与えない限り物体間の距離は長くあろうとすることがない。)
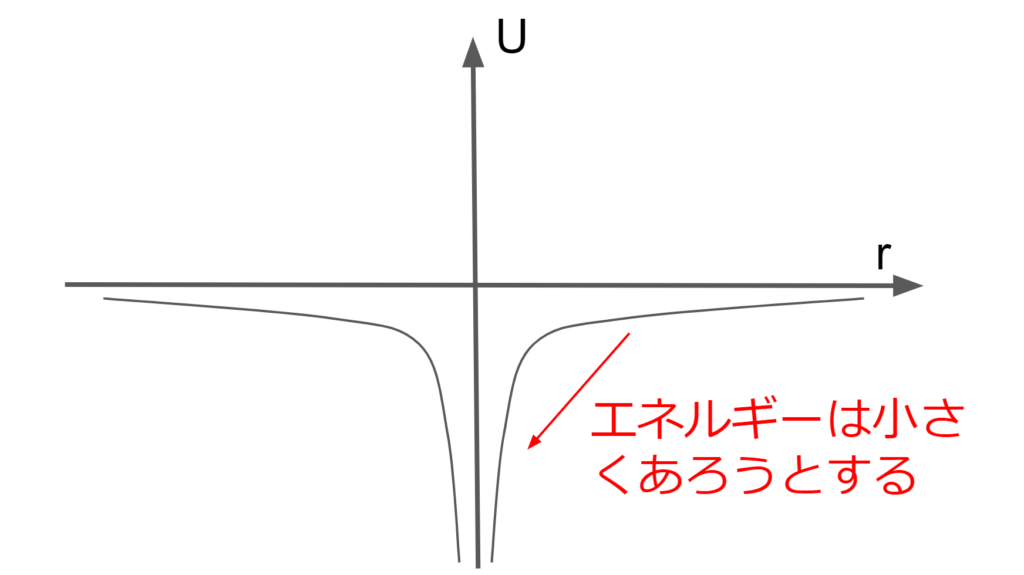
よって、2物体は互いに距離を縮めて束縛しあおうとするのである。
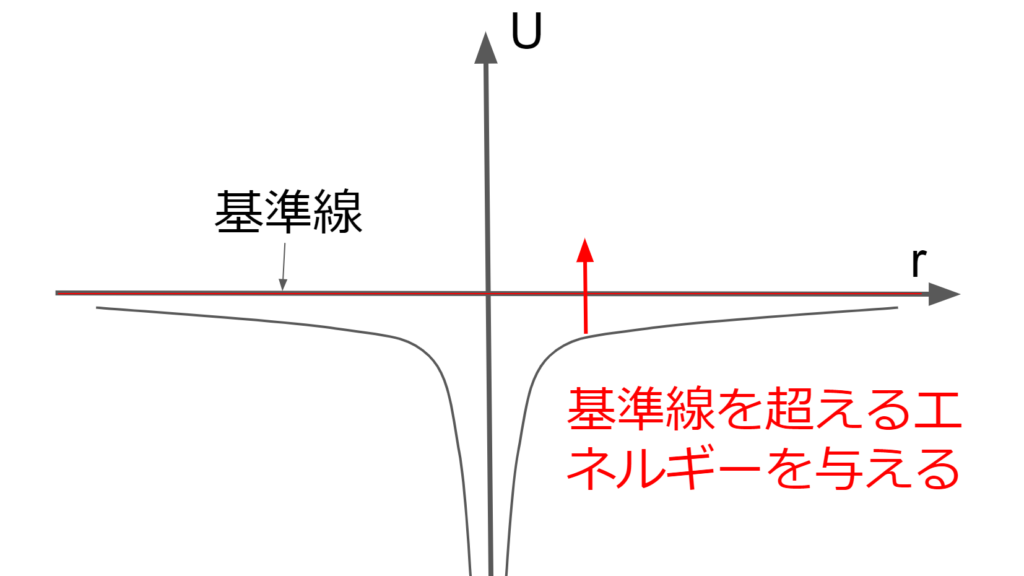
では、2つの物体を引き離すためにはどうすれば良いのか。
それは、物体を束縛しようとする位置エネルギーの基準点を超えるエネルギーを与えることである。
例えば、地球からロケットを飛ばそうとする。
つまり、ロケットを地球の束縛から解放させようとする。
地球の質量を\(M\)、半径を\(R\)、ロケットの質量を\(m\)とすると位置エネルギー\(U\)は以下になる。
\begin{eqnarray}
U=-G\frac{Mm}{R}
\end{eqnarray}
この時、ロケットを発射させる時に初速度\(v_0\)の運動エネルギーを与える。
この時の運動エネルギーと位置エネルギーの和である力学的エネルギーが位置エネルギーの基準点を超える時ロケットは地球の遥か彼方まで飛んでいく。
よって、以下を満たす時である。
\begin{eqnarray}
-G\frac{Mm}{R^2}+\frac{1}{2}mv_0^2\geq0
\end{eqnarray}
等号を満たす時の初速度\(v_0\)を第二宇宙速度と呼ぶ。
ケプラーの法則
太陽系では、太陽の周りを惑星が回っている。
これらの運動に置いて不変な法則を3つ説明する。(ケプラーの法則)
第一法則
惑星は太陽を焦点とした楕円軌道を描く。
第二法則
太陽と惑星を結ぶ線分が単位時間に描く面積は一定である。(面積速度一定)
第三法則
惑星の公転周期の2乗と楕円軌道の長半径の3乗の比は惑星の種類に依らず一定である。
\begin{eqnarray}
\frac{T^2}{a^3}&=&C\\
\\
T&:&公転周期\\
a&:&楕円軌道の長半径\\
C&:&定数
\end{eqnarray}
【楕円の関数】

