物体が動き始めるときは必ず力が働く。
この物体の運動の状態を考えるために必要なのが運動方程式である。
運動方程式を解くことで物体の運動(変位\(x\)や速度\(v\))を求めることができる。
だが、運動方程式は考える座標系によって異なる場合がある。
それは座標系同士が相対運動をしている時である。
様々な座標系についての運動方程式を考える必要がある。
本記事では物体に力が働いた時の運動とそれらを記述する運動方程式について説明する。
ニュートンの運動の法則
慣性の法則
慣性の法則とは、物体には現在の運動状態(速度)を保とうとする性質があり、この性質を慣性と呼ぶ。
つまり、静止している物体は静止し続けようとし、運動している物体はその運動を続けようとする。
以下の図で慣性の法則の例を見てもらう。
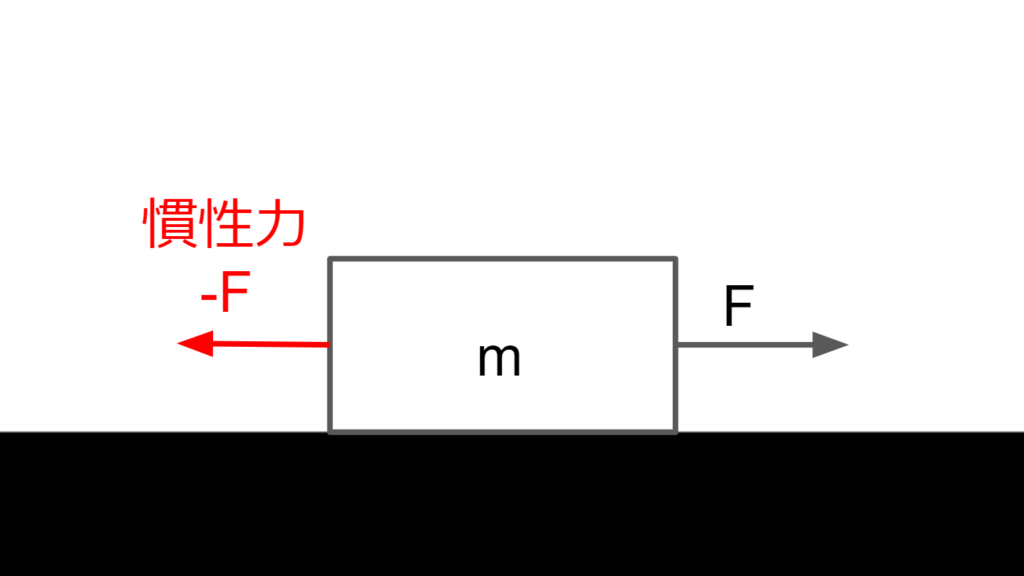
物体を力\(F\)で動かす。
この時、自分は物体の外から見ている。
この時、物体にかかる力は\(F\)である。
しかし、物体に乗って物体を見てみると、物体は運動をしていない。
よって、物体にかかる力は\(0\)である。
これは、物体に乗ると見かけ上の力である慣性力\(-F\)が物体にかかるからである。
慣性系
慣性の法則が成立する座標系を慣性系と呼ぶ。
【座標系とは】
慣性力
慣性力とは観測しているある座標系Ⅰが加速度\(a\)で加速度運動をしている時、座標系Ⅰにある物体には見かけ上の力である慣性力が働く。
この慣性力は加速度の方向と逆方向に働き、大きさは以下である。
\begin{eqnarray}
ma
\end{eqnarray}
先の図では物体の外から見ている座標系が座標系Ⅰに対応して、物体に乗っている座標系が座標系Ⅱに対応する。
座標系Ⅱは加速度\(\frac{F}{m}\)であるので、慣性力は\(-F\)であることが分かる。
運動の法則
運動方程式
物体に働く力\(\overrightarrow{F}\)と加速度\(\overrightarrow{a}\)の間には以下の関係が成立する。
\begin{eqnarray}
m\overrightarrow{a}=\overrightarrow{F}\\
\\
m:質量
\end{eqnarray}
力は加速度に比例して、この時の比例係数を質量と呼ぶ。
この方程式を運動方程式と呼ぶ。
加速度\(\overrightarrow{a}\)は以下の関係も成立する。
\begin{eqnarray}
\overrightarrow{a}=\frac{d\overrightarrow{v}}{dt}=\frac{d^2\overrightarrow{x}}{dt^2}
\end{eqnarray}
よって、運動方程式を時間\(t\)について不定積分をすることで変位\(\overrightarrow{x}\)と速度\(\overrightarrow{v}\)を求めることができる。
【不定積分の方法】
運動方程式は運動量を微分することで求まる。
運動量\(\overrightarrow{p}\)は以下である。
\begin{eqnarray}
\overrightarrow{p}=m\overrightarrow{v}\\
\\
m:質量\\
\overrightarrow{v}:速度
\end{eqnarray}
運動量の時間変化(つまり、運動量の時間微分)は力である。
よって、この運動量を\(t\)について微分すると以下になる。
\begin{eqnarray}
\frac{d}{dt}\overrightarrow{p}=m\frac{d\overrightarrow{v}}{dt}=\overrightarrow{F}
\end{eqnarray}
これは、紛れもなく運動方程式である。
運動方程式を立てる時の注意点
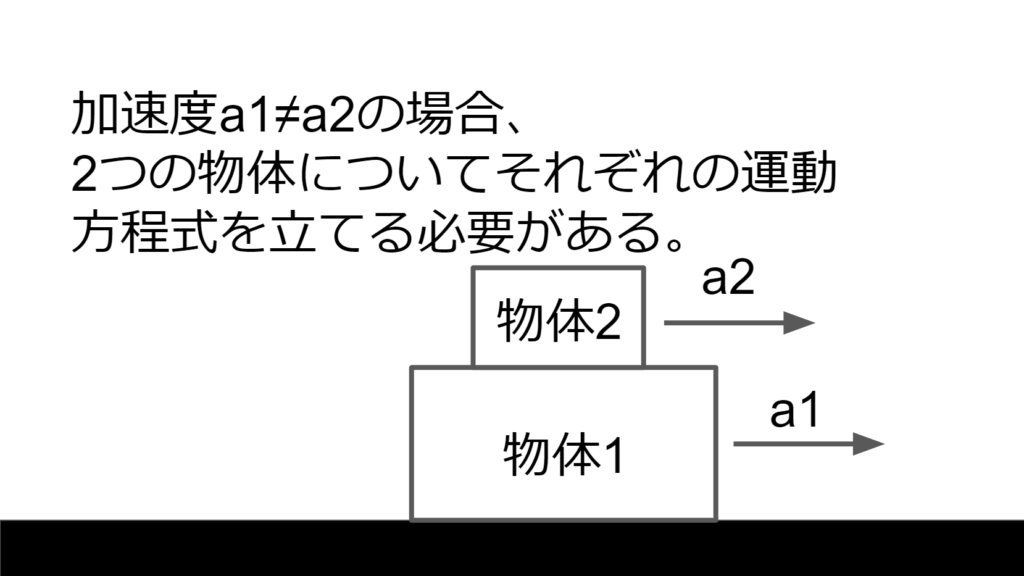
2つ以上の物体が一体となって運動をしているときは、個々の物体で見ても複数の物体を1つとして見ても加速度は等しいので個々の物体でも複数の物体を1つにした物体で運動方程式を立てても構わない。
しかし、2つ以上の物体が相対運動(次章説明)している時は、個々の物体で加速度が異なるので、別々に運動方程式を建てなくてなならない。
作用反作用の法則
物体\(A\)が物体\(B\)に働く力を及ぼしている時、物体\(B\)は力の大きさは等しく、逆方向に物体\(A\)に力を及ぼす。
この法則を作用反作用の法則と呼ぶ。

相対運動
ある座標系Ⅰから別の座標系Ⅱを見た時に、座標系Ⅱ全体が座標系Ⅰを動いている時、座標系Ⅰと座標系Ⅱは相対運動をしている。
例)
電車の窓から外の景色を見ると、外の景色は動いて見える。
だが、電車の外に出ると外の景色は動いていない。
前者では電車の中という座標系から外の景色を見ており、後者では電車の外という座標系から外の景色を見ている。
電車は電車の外に対して相対運動をしていることが分かる。
相対運動の特徴は座標系毎に運動方程式が異なる点である。
つまり、座標系毎に運動の状態が変わるのである。
運動の状態が変わるということは座標系によって速度や加速度が変わるということである。
それぞれを相対速度、相対加速度と呼ぶ。
それらを次節で説明する。
相対速度
座標系\(A\)が速度\(v_A\)、座標系\(B\)が速度\(v_B\)で運動をしている時、座標系\(A\)から座標系\(B\)を見た時の速度\(v_{AB}\)は以下になる。
\begin{eqnarray}
v_{AB}=v_B-v_A
\end{eqnarray}
相対加速度
座標系\(A\)が加速度\(a_A\)、座標系\(B\)が加速度\(a_B\)で運動をしている時、座標系\(A\)から座標系\(B\)を見た時の加速度\(a_{AB}\)は以下になる。
\begin{eqnarray}
a_{AB}=a_B-a_A
\end{eqnarray}

