力の釣り合いとは物体に働く力(又はモーメント)が0であり物体が静止している状態のことを言う。
力の釣り合いを考えるには物体にどんな力が働いているかを知る必要がある。
よって、様々な力の種類を前もって知ることが力の釣り合いを考える上で重要である。
本記事では力の釣り合いと様々な力の種類について説明する。
力の釣り合い
物体に働く力が釣り合っている状態とは物体に働く力(もしくはモーメント)が0であり静止している状態のことを言う。
運動方程式で記述すると以下になる。
\begin{eqnarray}
m\frac{d^2\overrightarrow{x}}{dt^2}&=&F_1+F_2+F_3+\cdots+F_n\\
\\
&=&\overrightarrow{0}
\end{eqnarray}
力の釣り合いを考える時は\(F_1,F_2\cdots,F_n=0\)を記述することが必要になる。
ここで、力の釣り合いを考える上で重要なのは、以上にある\(F_1,F_2\cdots,F_n\)の力を正しく記述することができるかどうかである。
物体に働く力を正しく理解していなければ力の釣り合いを考えることはできない。
つまり、力の釣り合いを考えるには様々な力の種類を知っておく必要がある。
次章では様々な力の種類について説明する。
【運動方程式とは】
【物体のモーメントとは】
様々な力の種類
摩擦力(friction)
摩擦力は接触している物体同士が相対運動を起こそうとする時に、接触面に働く抵抗力である。
摩擦力には2種類ある。
静止摩擦力
静止摩擦力とは物体が静止するように外力(物体を動かそうとする力)に対して働く力である。
静止摩擦力は以下になる。
\begin{eqnarray}
F_{s}&=&F\\
\\
F_s&:&静止摩擦力\\
F&:&外力
\end{eqnarray}
だが、静止摩擦力には上限が存在する。
この静止摩擦力の上限を最大静止摩擦力と呼び、以下を満たす。
\begin{eqnarray}
F_{max}&=&\mu_{s}N\\
\\
F_{max}&:&最大静止摩擦力\\
\mu_{s}&:&静摩擦係数\\
N&:&垂直抗力
\end{eqnarray}
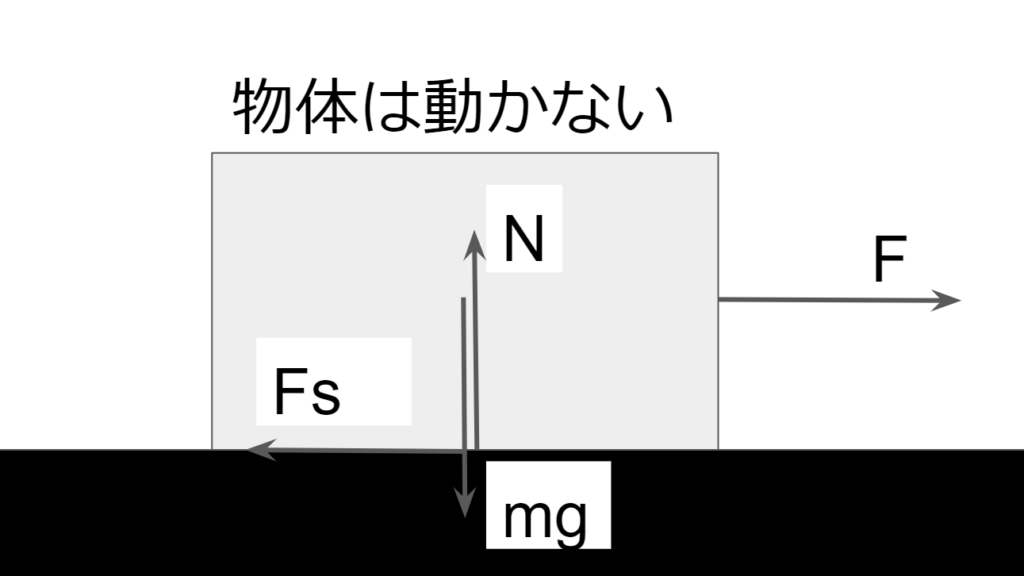
最大静摩擦力は物体同士の接触面に垂直な抗力である垂直抗力に比例する。
この時の比例係数を静摩擦係数と呼ぶ。
動摩擦力
動摩擦力とは物体同士が相対運動をしている時に接触面に働く抵抗力である。
動摩擦力は以下を満たす。
\begin{eqnarray}
F_d&=&\mu_{d}N\\
\\
F_d&:&動摩擦力\\
\mu_d&:&動摩擦係数\\
N&:&垂直抗力
\end{eqnarray}
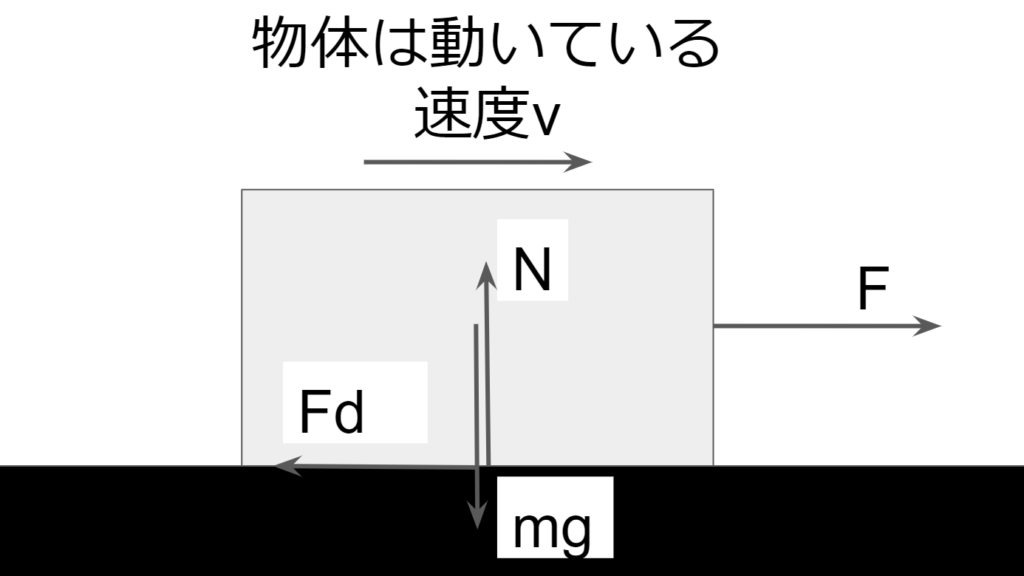
動摩擦力は物体同士の接触面に垂直な抗力である垂直抗力に比例する。
この時の比例係数を動摩擦係数と呼ぶ。
一般的に動摩擦係数は運動している物体の速度に依らない。
一般的に静摩擦係数と動摩擦係数の間には以下の不等式を満たす。
\begin{eqnarray}
\mu_s>\mu_d
\end{eqnarray}
張力(tension)
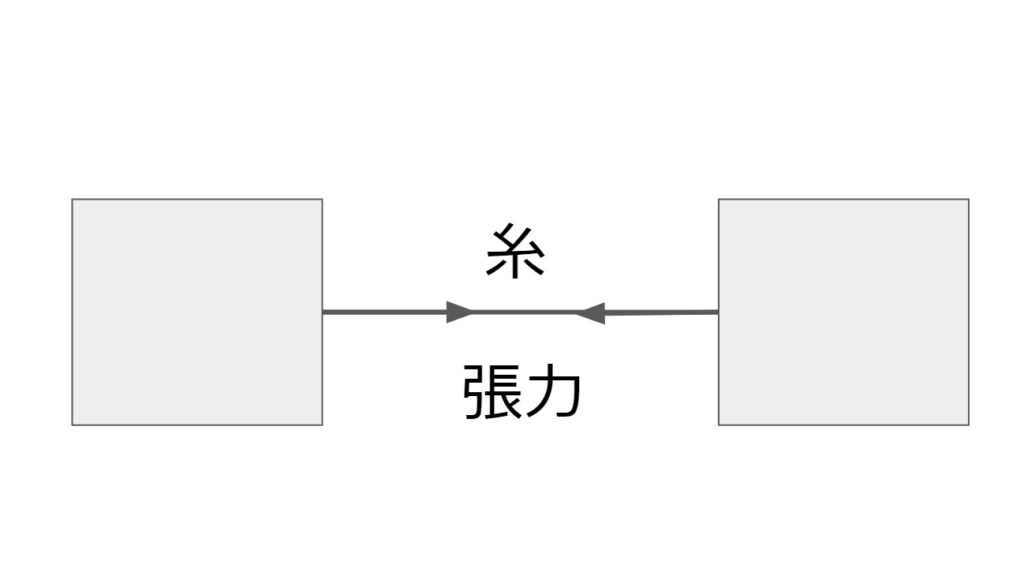
張力は糸が物体とつながっている時に、物体を引っ張る方向に働く力である。
この時、糸は張っている。
浮力(buoyancy)
浮力は液体中の物体に鉛直上向き方向に働く力である。
浮力は以下を満たす。
\begin{eqnarray}
F_b&=&V\rho g\\
\\
F_b&:&浮力\\
V&:&物体が液体を押しのけた体積\\
\rho&:&液体の密度\\
g&:&重力加速度
\end{eqnarray}
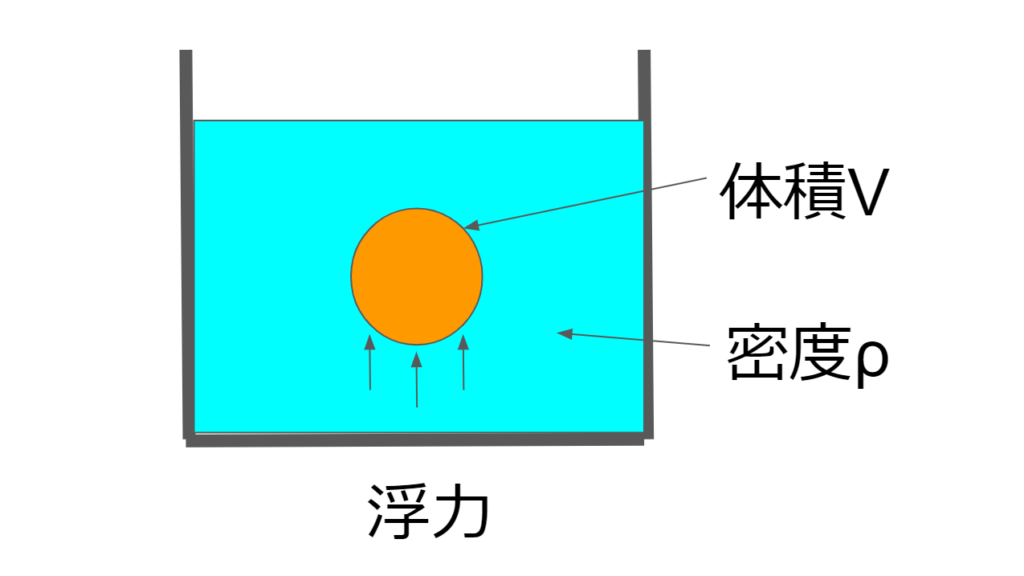
浮力は物体が押し出した液体の体積と液体の密度で決まる。
(重力加速度は一定)
バネの弾性力
バネの弾性力はバネに力が働いていない時の長さ(自然長)から、バネが伸びたり縮んだりすることで働く力である。
バネが伸びる方向を正とするとバネの力は以下を満たす。
\begin{eqnarray}
F_k&=&-k\Delta x\\
\\
F_k&:&バネの弾性力\\
k&:&バネ定数\\
\Delta x&:&バネの変形量
\end{eqnarray}
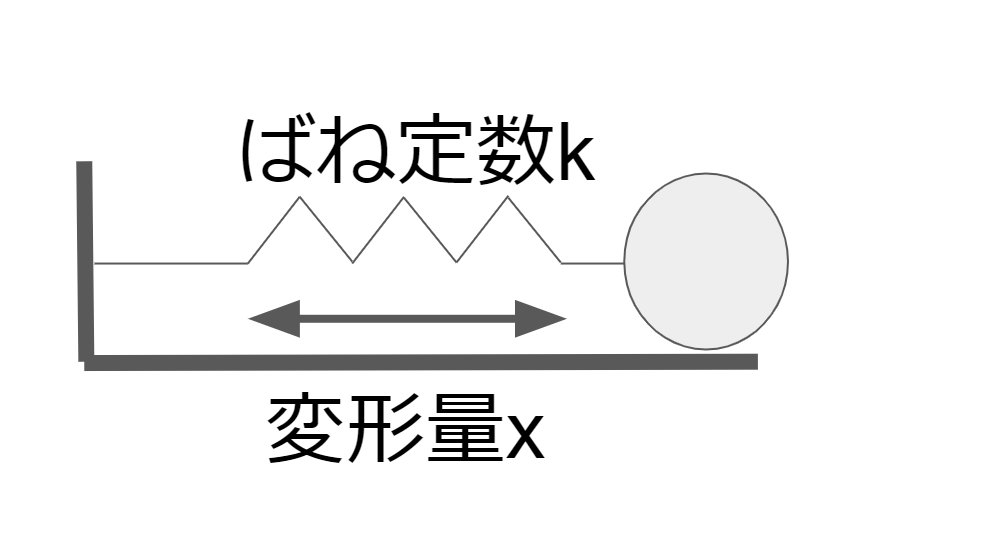
バネの弾性力はバネの変形量に比例する。
この時の比例係数をバネ定数と呼ぶ。(フックの法則)
バネ定数はバネによって異なる。
滑車
滑車は力の大きさはそのまま似して力の方向を変えることができる。
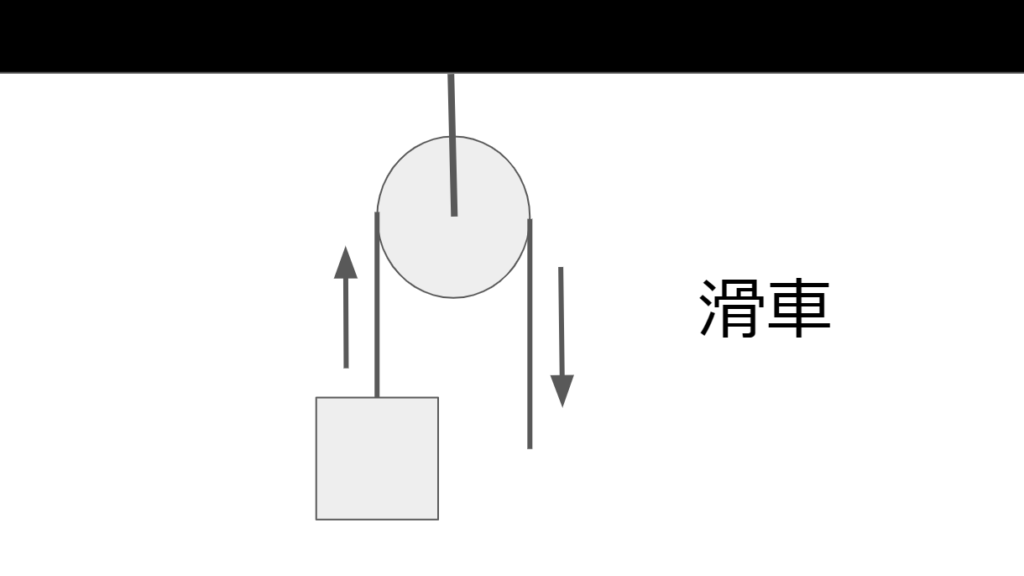
また、動滑車は引く力を半分にする。
動滑車にかかる力の釣り合いを考える。
2つの糸の張力\(T\)とぶら下がっている物体の重力より以下の等式を満たす。
\begin{eqnarray}
2T&=&mg\\
\\
T&=&\frac{mg}{2}
\end{eqnarray}
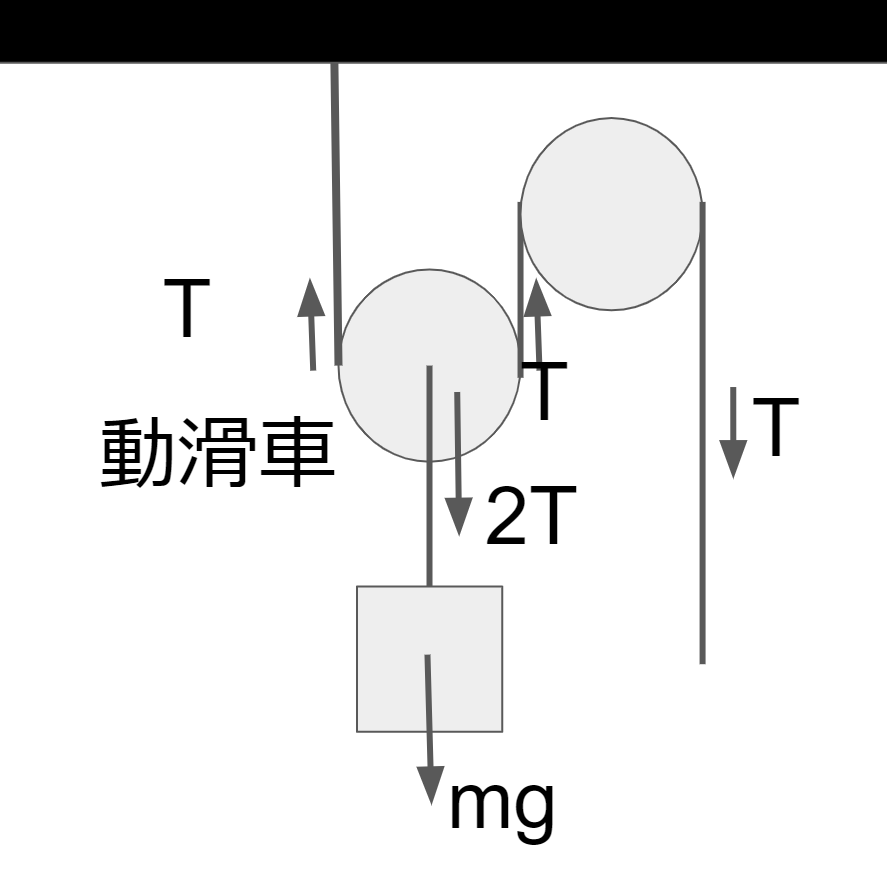
よって、人が糸を引く力は\(\frac{mg}{2}\)で物体の重さの半分になる。

