等加速度直線運動は高校物理で最初に学ぶ物理の単元である。
等加速度直線運動はその名の通り、物体が加速度一定で直線に進む運動である。
等加速度直線運動の公式はいくつかあるが、運動方程式のみ押さえれば問題は解くことができる。
本記事では、本来高校物理では扱わない微分積分を用いた考えを紹介する。
公式を暗記するより運動方程式を正しく立てることができれば等加速度運動の問題は解くことができる。
等加速度直線運動について説明する。
等加速度直線運動
等加速度直線運動とは加速度が一定(時間変化しない)である運動である。
つまり、物体にかかる力が一定である運動である。
運動方程式で表すと以下になる。
\begin{eqnarray}
m\frac{d^2\overrightarrow{x}}{dt^2}=F\\
\\
F:tに依らない定数\\
m:物体の質量\\
\overrightarrow{x}:物体の変位\\
t:時間
\end{eqnarray}
この運動方程式を\(t\)について1回積分することで速度\(v(t)\)、2回積分すると変位\(x(t)\)を求めることができる。
例)
自由落下、鉛直投げ上げ、etc
速度、加速度とは
速度
速度(velocity)は慣例として\(v\)と表す。
速度\(v\)の定義は以下である。
\begin{eqnarray}
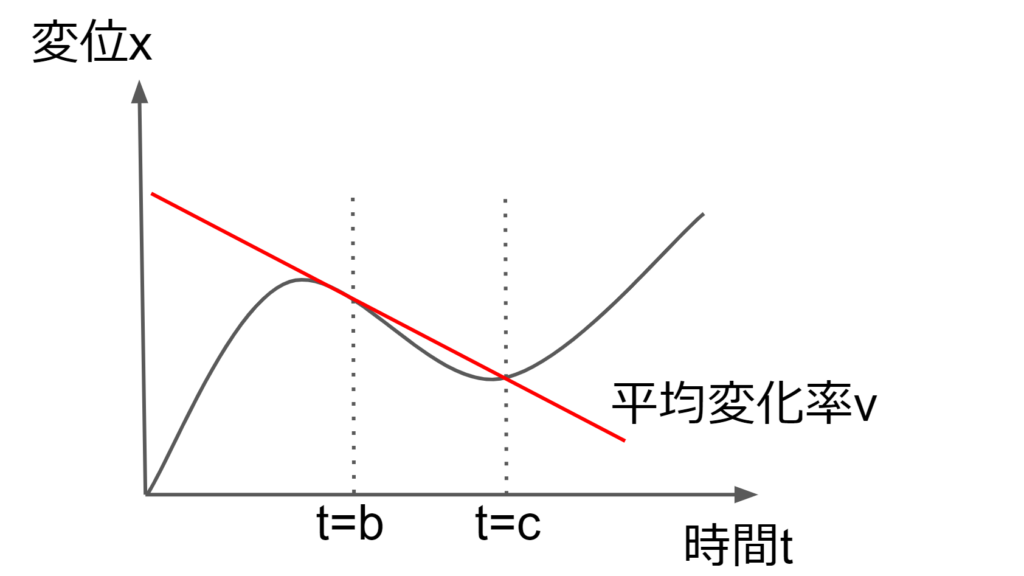
v=\frac{x(c)-x(b)}{c-b}
\end{eqnarray}
\(x\)は物体の変位(位置)である。
この速度\(v\)を\(x-t\)グラフで見ると曲線の\(t=b\)から\(t=c\)までの平均変化率であることが分かる。
また、速度\(v\)を以下のようにも表すことができる。
\begin{eqnarray}
v=\frac{x(t+t’)-x(t)}{t’}
\end{eqnarray}
この時、\(t’\)を0に限りなく近づけると以下になる。
\begin{eqnarray}
v&=&\lim_{t’ \to 0}\frac{x(t+t’)-x(t)}{t’}\\
\\
&=&\frac{dx}{dt}
\end{eqnarray}
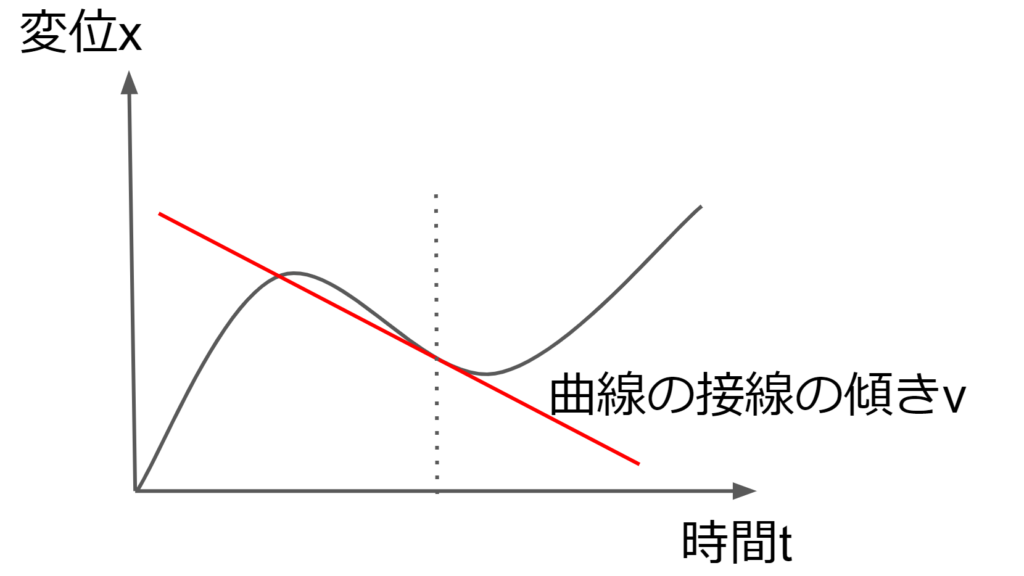
よって、速度\(v\)は物体の変位\(x\)の導関数であることが分かる。
\(x-t\)グラフで見ると速度\(v\)は曲線上の点\((t,x(t))\)の接線の傾きであることが分かる。
【導関数とは】
\(x-t\)グラフ
\(x-t\)グラフとは横軸に時間\(t\)、縦軸に物体の変位\(x\)とした時のグラフである。
つまり、物体の変位\(x\)の時間変化を表したグラフである。
\(x-t\)グラフでは曲線上のある時間\(t\)での接線の傾きは時間\(t\)での速度\(v\)と等しい。
加速度
加速度(acceleration)は慣例として\(a\)と表す。
加速度の定義は以下である。
\begin{eqnarray}
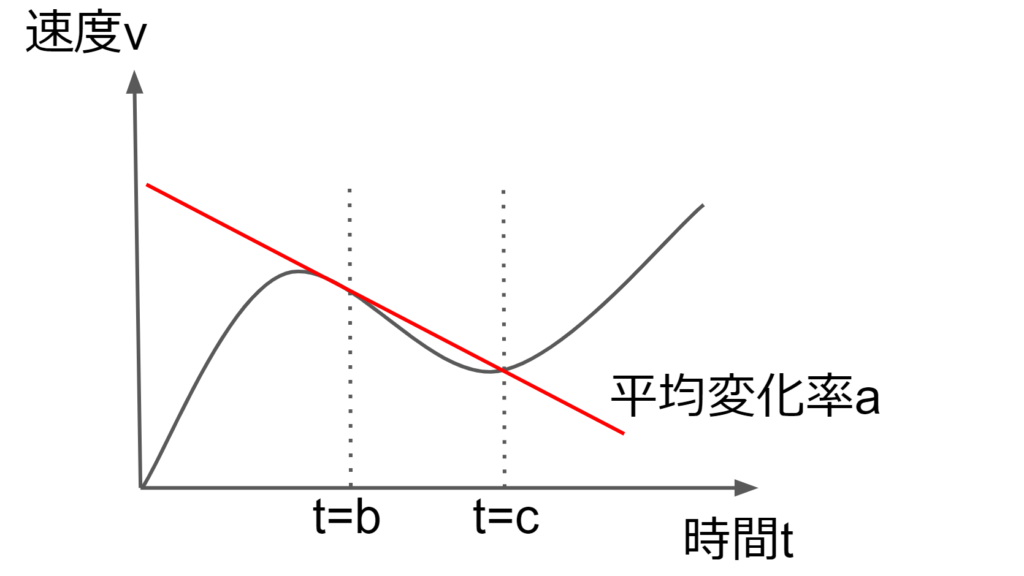
a=\frac{v(c)-v(b)}{c-b}
\end{eqnarray}
\(v\)は物体の速度である。
この加速度\(a\)を\(v-t\)グラフで見ると曲線の\(t=b\)から\(t=c\)までの平均変化率であることが分かる。
また、加速度\(a\)を以下のようにも表すことができる。
\begin{eqnarray}
a=\frac{v(t+t’)-v(t)}{t’}
\end{eqnarray}
この時、\(t’\)を0に限りなく近づけると以下になる。
\begin{eqnarray}
a&=&\lim_{t’ \to 0}\frac{v(t+t’)-v(t)}{t’}\\
\\
&=&\frac{dv}{dt}(=\frac{d^2x}{dt^2})
\end{eqnarray}
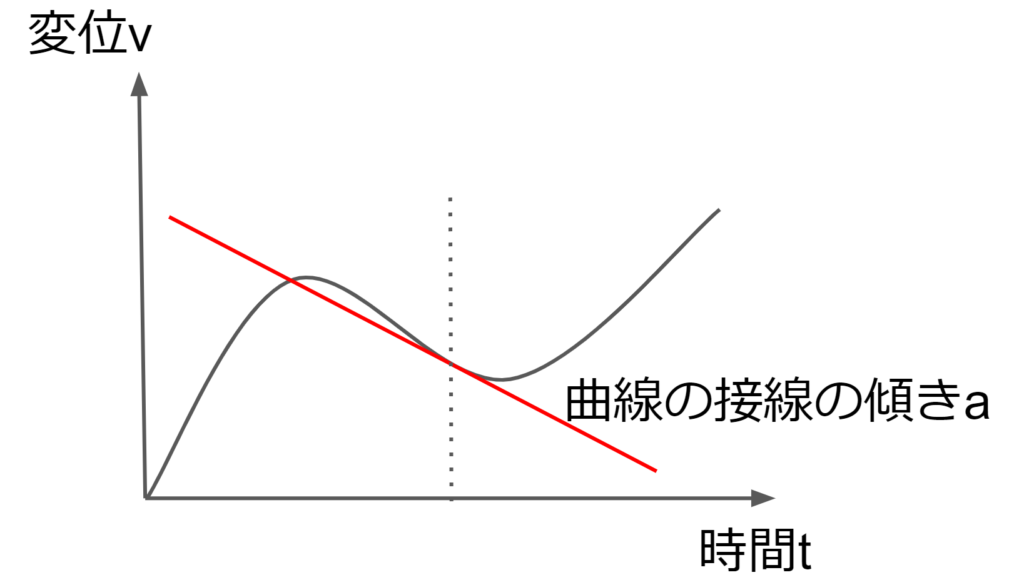
よって、加速度\(a\)は物体の速度\(v\)の1次導関数であり、変位\(x\)の2次導関数であることが分かる。
\(v-t\)グラフで見ると加速度\(a\)は曲線上の点\((t,v(t))\)の接線の傾きであることが分かる。
【導関数とは】
\(v-t\)グラフ
\(v-t\)グラフとは横軸に時間\(t\)、縦軸に物体の速度\(v\)とした時のグラフである。
つまり、物体の速度\(v\)の時間変化を表したグラフである。
\(v-t\)グラフでは曲線上のある時間\(t\)での接線の傾きは時間\(t\)での加速度\(a\)と等しい。
また、\(x=a\)、\(x=b\)、\(t\)軸、曲線に囲まれた部分の面積は物体が時間\(t=b\)から\(t=c\)の間に進んだ移動距離に等しい。
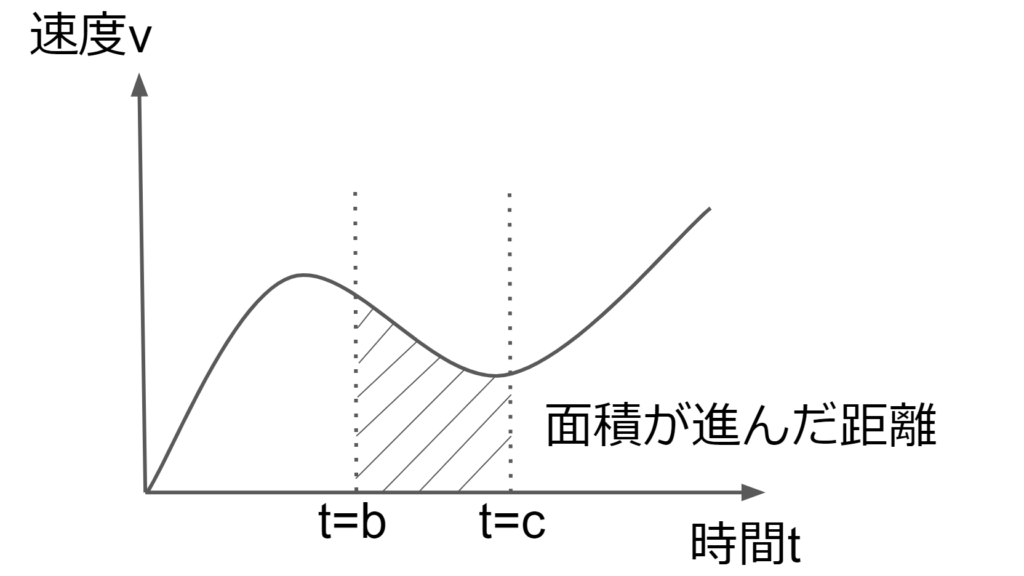
以上の斜線部の面積を求めるには曲線\(v(t)\)を\(t=b\)から\(t=c\)まで積分すると求めることができる。
式は以下になる。
\begin{eqnarray}
x=\int_{b}^{c}v(t)dt
\end{eqnarray}

